Figure it Out (Page 152)
Fill in the blanks with fractions.
1. Three guavas together weigh 1 kg. If they are roughly of the same size, each guava will roughly weigh __1/3__ kg.
2. A wholesale merchant packed 1 kg of rice in four packets of equal weight. The weight of each packet is __1/4__ kg.
3. Four friends ordered 3 glasses of sugarcane juice and shared it equally among themselves. Each one drank ____ glass of sugarcane juice.
Solution :
Amount of sugarcane consumed by four friends = 3 glasses .
Amount of sugarcane consumed by each friend =
4. The bis fish weighs
Solution:

Given the weighs of big fish = 1/2 kg and the weighs of small fish = 1/4 kg
Total weight of both fish =
= 3/4 kg
Figure it Out (Page 155)
1. The figures below show different fractional units of a whole chikki. How much of a whole chikki is each piece?
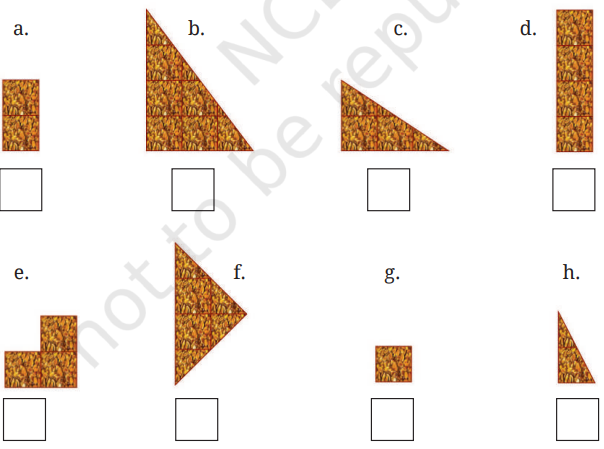
Solution:
(a) We get this piece by breaking the chikki into 12 equal parts. Hence it is 1/2
(b) We get this piece by breaking the chikki into 4 equal parts. Hence it is 1/4
(c) We get this piece by breaking the chikki into 8 equal parts. Hence it is 1/8
(d) We get this piece by breaking the chikki into 6 equal parts. Hence it is 1/6
(e) We get this piece by breaking the chikki into 8 equal parts. Hence it is 1/8
(f) We get this part by breaking the chikki into 6 equal pieces. Hence it is 1/6
(g) We get this part by breaking the chikki into 24 equal pieces. Hence it is 1/24
(h) We get this part by breaking the chikki into 24 equal pieces. Hence it is 1/24
Figure it Out (Page 158)
1. Continue this table of
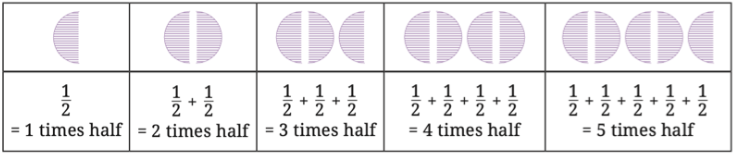
Solution:

2. Can you create a similar table for
Solution: Yes, we can create a similar table for 1/4. Here
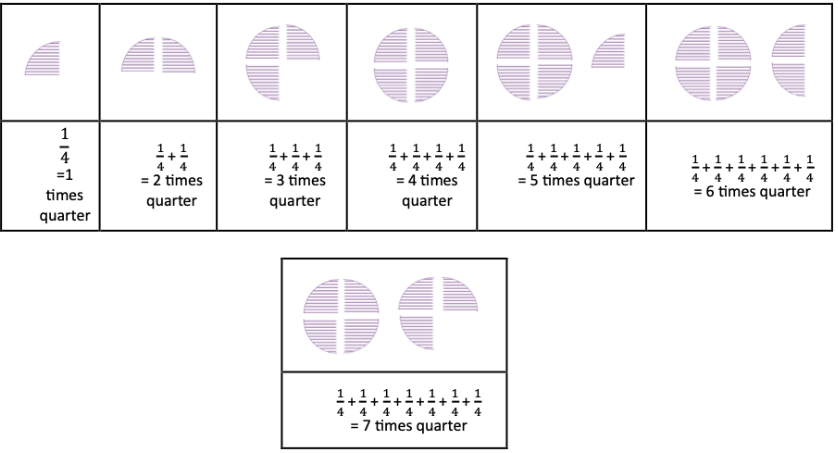
3. Make
Solution:
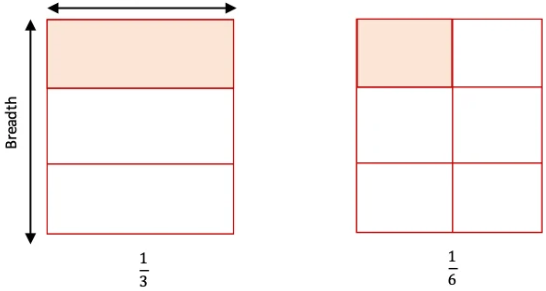
Fold the pa per strip along the length into 3 equal sections and each section represents
Fold the pa per strip again in half breadthwise there by creating 6 equal sections and each section represents
4. Draw a picture and write an addition statement as above to show:
(a) 5 times
Solution:
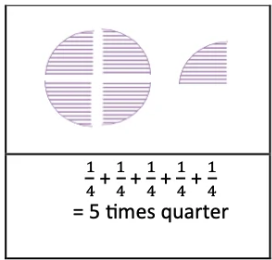
(b) 9 times
Solution:
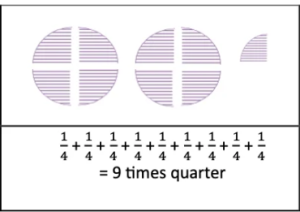
5. Match each fractional unit with the correct picture :
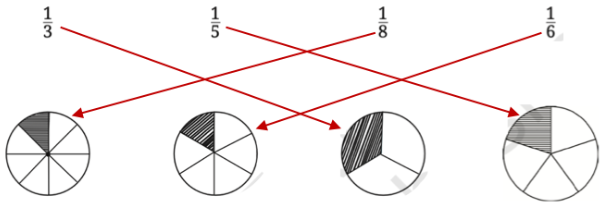
Figure it Out (Page 160)
1. On a number line, draw lines of lengths
Solution:
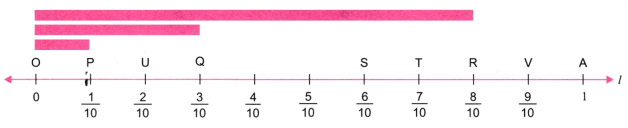
Step 1. Draw a line l. Mark a point O on it.
Step 2. Mark point A at a distance of 1 unit from O.
Step 3. Divide OA into 10 equal parts.
Here OP represents
OQ represents
OR represents
2. Write five more fractions of your choice and mark them on the number line.
Solution:
Step 1. Let a number line OJ is divided into 10 equal parts.
Step 2. Now mark points A, B, C, D,…., J on it.
Step 3. Here
OF represents
OG represents
OB represents
OH represents
OI represents
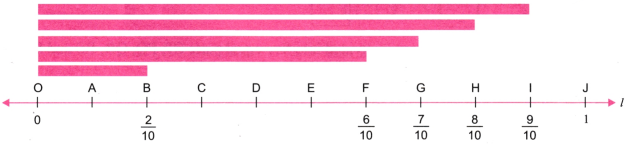
3. How many fractions lie between 0 and 1 ? Think, discuss with your classmates, and write your answer.
Solution:
There are an infinite number of fractions between 0 and 1.
Example:
4. What is the length of the pink line and black line shown below? The distance between 0 and 1 is 1 unit long, and it is divided into two equal parts. The length of each part is 1/2. So the pink line is y units long. Write the fraction that gives the length of the black line in the box.

Solution:
Length of black line is
Length of black line is
Fraction that gives length of black line =
5. Write the fraction that gives the lengths of the black lines in the respective boxes.
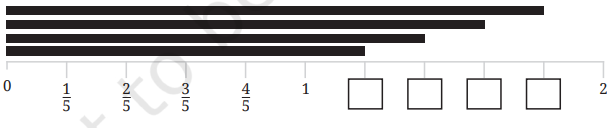
Solution:

Figure it Out i (Page 162)
1. How many whole units are there in
Solution: Here
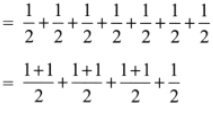
= 1 + 1 + 1 +
= 3 +
=
Hence 3 whole units are there in
2. How many whole units are there in
Solution:
Here
=
= 1 +
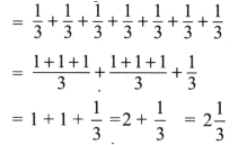
Hence 1 whole unit are there in
Figure it Out ii (Page 162)

Solution:

2. Can all fractions greater than 1 be written as such mixed numbers?
A mixed number /mixed fraction contains a whole number (called the whole part) and a fraction that is less than 1 (called the fractional part).
Solution:
Yes, all fractions greater than 1 can be written as mixed fractions/numbers.
3. Write the following fractions as mixed fractions (e.g.,
Solution:
(a)

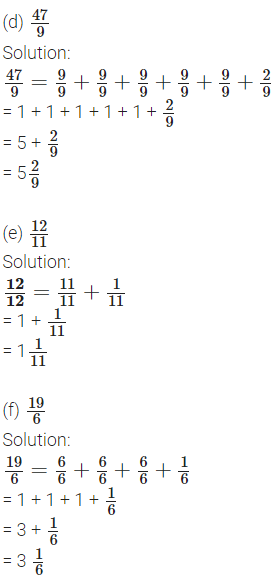
Figure it Out (Page 163)
1. Write the following mixed numbers as fractions:
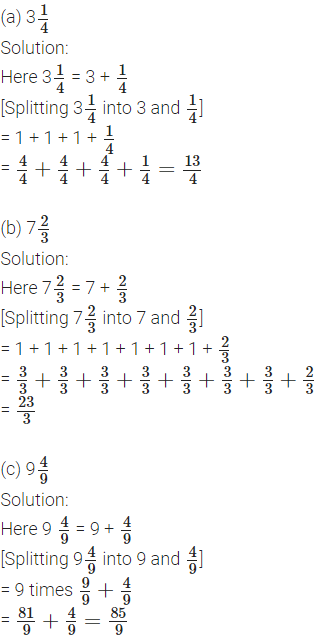
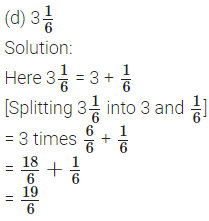
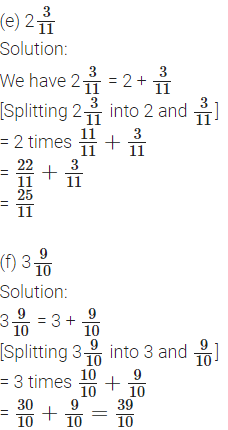
Figure it Out (Page 165)

3.
(Write as many as you can)
Solution:
Here,
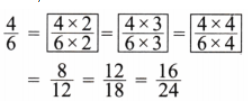
Figure it Out (Page 166)
1. Three rods are shared equally by four children. Show the division in the picture and write a fraction for how much each child gets. Also, write the corresponding division facts, addition facts and multiplication facts.
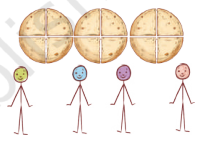
Fraction of roti each child gets is _________________ .
Division fact:
Addition fact:
Multiplication fact:
Compare your picture and answers with your classmates!
Solution:
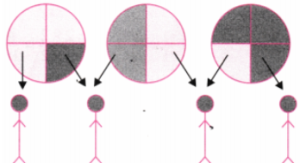

2. Draw a picture to show how much each child gets when 2 rotis are shared equally by 4 children. Also, write the corresponding division facts, addition facts, and multiplication facts.
Solution:
As 2 rotis have to be shared equally by 4 children we divide each roti in 4 parts and give
(a) 1 part of each roti to each child as shown below:
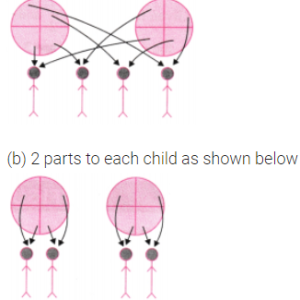
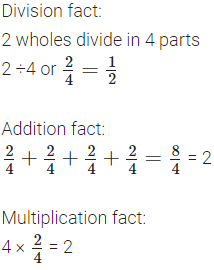
Figure it Out (Page 168, 169)
1.Find the missing numbers:
(a) 5 glasses of juice shared equally among 4 friends is the same as _______ glasses of juice shared equally among 8 friends. So,
(b) 4 kg of potatoes divided equally in 3 bags is the same as 12 kgs of potatoes divided equally in ______ bags. So,
(c) 7 rods divided among 5 children is the same as rods divided among children. So,
Solution:
(a) Here, the amount of juice each friend gets when 5 glasses are shared among 4 friends
=
Now to determine how many glasses of juice would be needed to give each of the 8 friends the same amount = 8 × 5/4
= 10 glasses
So, 10 glasses of juice shared equally among 8 friends is the same as 5 glasses of juice shared equally among 4 friends.
Therefore

(Page 172)
1. Find equivalent fractions for the given pairs of fractions such that the fractional units are the same.




Figure it Out (Page 173)
1. Express the following fractions in lowest terms:


Figure it Out (Page 174)
1. Compare the following fractions and justify your answers:
(a)
Solution:
(a) Given fractions are
Here LCM of denominators 3 and 2 is 6 then multiplying and dividing 8/3 by 2 and 5/2 by 3 then
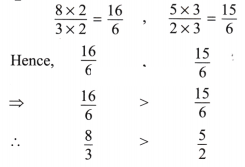
(b)
Solution: Given fractions are
then multiplying and dividing
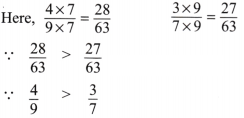
(c)
Solution: Given fractions are
then multiplying and dividing


2. Write following fractions ascending order.
(a)
Solution: The given fractions are
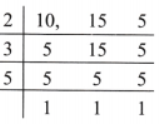
∴ LCM of 10, 15 and 5 = 2 × 3 × 5 = 30
Now let us make denominator of each fractions as LCM
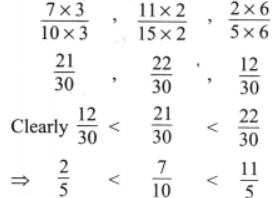
Hence given fractions in ascending order are:
(b)
Solution:
The given fractions are
Here LCM of 24, 6, 12 is 24.
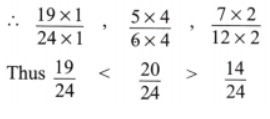
On arranging in ascending Order, we get
⇒
3. Write the following fractions descending order.
(a)
Solution:

(b)
Solution:

Figure it Out (Page 179)
1. Add the following fractions using Brahmagupta’s method:
(a)
Solution:
Here
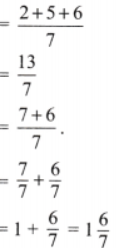
(b)
Solution:
Here
Here LCM of denominators 4 and 3 is 12
∴ Equivalent fraction of
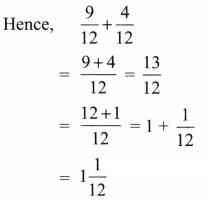
(c)
Solution:
Given
Now LCM of 3 and 6 is 6.
Expressing as equivalent fractions with denominators 6, we get
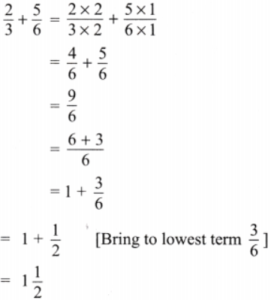
(d)
Solution:
Here
Now LCM of 3 and 7 is 21
Expressing as equivalent fractions with denominators 21, we get
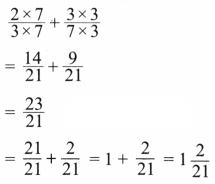
(e)
Solution:
Here
Now LCM of 4, 3, 5 is 60.
Expressing as equivalent fractions with denominators 60, we get
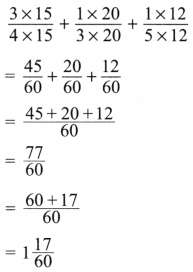
(f)
Solution:
Here
Now LCM of 3 and 5 is 15
Expressing as equivalent fractions with denominators 15, we get
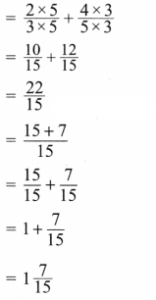
(g)
Solution:
Here
Now LCM of 5 and 3 is 15
Thus expressing as equivalent fractions with denominators 15, we get
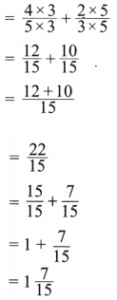
(h)
Solution:
Given
Here LCM of 5 and 8 is 40
Expressing as equivalent fractions with denominators 40, we get

(i)
Solution:
Here
Now LCM of 2 and 4 is 4.
Expressing as equivalent fractions with denominators 4, we get
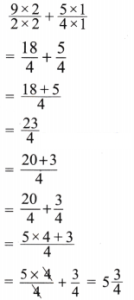
(j)
Solution:
Given
Here LCM of 3 and 7 is 21
Expressing as equivalent fractions with denominators 21, we get
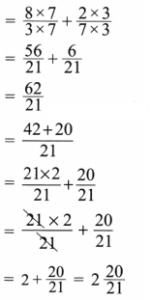
(k) Same as (e) Part
(l)
Solution:
Here
Now LCM of 3, 5 and 7 is 105.
Expressing as equivalent fractions with denominators 105, we get
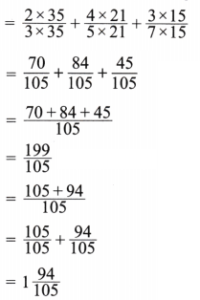
(m)
Solution:
Given
Here LCM of 2, 4, 6 is 12.
Now expressing as equivalent fractions with denominators 12, we get
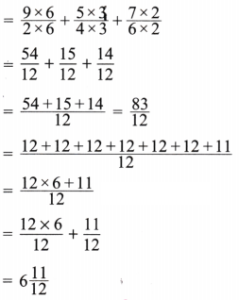
2. Rahim mixes
Solution:
Given quantity of yellow paint =
and quality of blue paint =
Volume of green paint made =
Here LCM of 3 and 4 is 12
Now expressing as equivalent fractions with denominator 12, we get
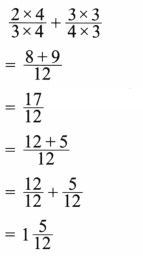
3. Geeta bought
Solution:
Given length of lace bought by Geeta =
and length of lace bought by Shamim =
Total length of lace =
LCM of 5 and 4 is 20
Now expressing as equivalent fractions with denominator 20, we get
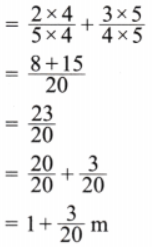
Total lace required = Perimeter = 1 m
Hence total lace Geeta and Shamim have together is sufficient to cover the whole border.
Figure it Out (Page 181)
1.
Solution:
Given
As fractional unit is same i.e., 18 we shall simply subtract numerators keeping fractional unit as
Then
=
2.
Solution:
Given
As fractional unit is same i.e.,
=
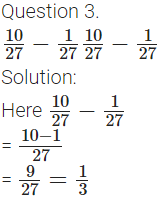
1. Carry out the following subtractions using Brahmagupta’s method:
(a)
Solution:

(c)

2. Subtract as indicated:
(a)
Solution:
Given y – y
Here, LCM of 3 and 4 is 12.
Fractional unit for both fractions should be
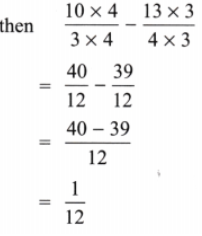
(b)
Solution:
Here,
Now, LCM of 3 and 5 is 15.
Fractional unit =
Hence
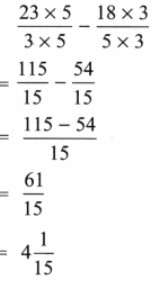
(c)
Solution:
Here fractional,
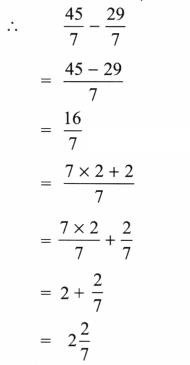
3. Solve the following problems:
(a) Java’s school is
and then walks the remaining distance to reach her school. How much does she walk daily to reach the school?
Solution:
Given distance between Jaya’s school and home is
and distance covered by Jaya in auto is
∴ Distance Jaya covered by walking =
LCM of 10 and 2 is 10.


No comments:
Post a Comment